Purdue CS352 Compiler Writeup
by Evan Shaw
Background
This compiler was created for Purdue CS352. The professor Li Zhiyuan adapted the class slides and project specifications from his graduate compilers course CS502. Students were required to complete five stages of the project, with each stage building on the codebase and the features of the last stage. If completed correctly, students should have come out of the course with a program that compiles MiniJava to semi-optimized 32-bit ARM assembly. The following is a description of my own codebase, and how I completed this task.
I believe that this project is the most difficult project I have ever completed. It took a substantial amount of time and effort to research and understand the algorithms and technical details that made this possible.
Table of Contents
- Tokenization
- Parsing
- Abstract Syntax Tree (AST) Construction
- Type/Reference Checking
- Symbol Table Construction
- Assembly Generation
- Three Address Code (3AC)
- Generating Three Address Code (3AC)
- Control Flow
- Calling Convention
- Function Calls
- Register Assignment
- Spilling
- Caller and Callee Saved Register Assignment Optimization
- Additional Optimizations Performed
- Additional Possible Optimizations
- Conclusion
Tokenization
Tokenization is the process of splitting a string of characters into discrete ‘tokens’ that each have an individual meaning. The tokenization process is mostly handled by flex (lex).
Parsing
After the tokenization is complete, the tokens are then fed into the parser. A parser is an algorithm which takes in tokens, and tries to match them using specific rules in a context-free grammar. The specific context-free grammar for this project is a small subset of Java which includes arithmetic operations, control flow (if, while), functions, and array operations. It is defined as follows:
To streamline the parsing process, we were required to use Yacc, or its more modern counterpart, Bison. The parser is defined in parser.y, a special Yacc file format. Each nonterminal is defined by its name followed by a colon.
This snippet defines a nonterminal of VarDecl:
A nonterminal definition consists of terminals and other nonterminals. The nonterminals in this specific declaration are Type, OptionalExp, and MoreVarDecl. The terminals are ID, which is a string of characters, and a semicolon. The terminals come directly from the tokenizer, so little to no string processing takes place in the parser.
This grammar rule matches variable declarations in the input code file. This grammar rule requires a Type (int, String, bool), followed by an ID (name of the variable), then an optional expression, which could either be an equals sign followed by a value, or empty. Following this comes an option to declare more variables in the same statement.
Once the parser has identified a grammar rule, it executes the C/C++ code in its definition. Most grammar rules contain code that results in a node being created to store details about the statement and its children. Yacc has a special syntax to reference these nodes. A $$ represents the node created by the current statement. A $1 represents the first terminal/nonterminal in the statement definition. The $1 here represents the node returned by the Type nonterminal.
After parsing the entire stream of tokens, the parser outputs a tree of nodes which correspond to the features of the context-free grammar. This is referred to as a Concrete Syntax Tree (CST) (put a link here to CST description) . (maybe also put in a picture of a CST)
Abstract Syntax Tree (AST) Construction
A Concrete Syntax Tree retains many extraneous details about the language’s grammar. These details are often unnecessary and hard to maneuver around when manipulating the tree for further processing. This is why it is necessary to simplify the CST into an Abstract Syntax Tree (AST). The AST abstracts many grammar-specific details.
For instance, when generating assembly code for expressions, it really is not necessary whether an expression node is a Factor, or a Term, it just matters its position relative to other expression nodes. The execution order of expressions is dictated by the structure of the tree and not what type of expression node it is. Another example of why generating an AST is better than leaving it in CST form is the ability to transform recursive leaves of trees into vectors held by a single AST node. For instance, the StatementsASTNode class contains a vector of StatementASTNode objects. This allows direct indexing of StatementASTNodes. This strategy also helps with control flow statements. In the IfElseStatementASTNode class, there are two private fields:
The consolidation from a CST tree form to an AST vector form allows much cleaner production of 3AC intermediate code from these control structures. Instead of referencing a left and right node, or node 0 and node 1, methods in the statement class can use the various pointers to vectors of the different logic results.
In ASTConstructor.cpp, the CST consisting of C structs is converted to the AST consisting of C++ objects. This is performed by doing a post-order tree traversal using the call stack to keep track of order.
The reason that C structs from the parser are being converted into C++ objects for the AST is because I took the parser from the previous C project I wrote, because it is difficult to get C++ to play nicely with bison.
During this process, the symbol table is constructed. More detail on this will be explained shortly.
Type/Reference Checking
Project 2 required Type and Reference Before Declaration checking. A Reference Before Declaration occurs when a programmer attempts to use or change a variable before it has been declared. This is easily checked when traversing through the AST to create the Symbol Table. If a variable reference is not in the Symbol Table, it is counted as a Reference Before Declaration.
Type checking is the process of verifying that expressions and functions have compatible inputs and outputs in terms of type. For example, in Java, it is possible to add a string to another string: variable1 = str1 + str2. This results in a concatenation. However, it is impossible to subtract a string from another string. Type checking during compilation ensures that all operations occur on compatible types.
The type checking code that was built for Project 2 was omitted in this codebase because type checking was not required for Project 5. All inputs are assumed to be valid MiniJava code.
Symbol Table Construction
A Symbol Table is a data structure that contains details of a program’s literals, variables and functions (this is not to be confused with symbol tables embedded in executable files, symbol table here refers to an internal compiler data structure).
As stated previously, the Symbol Table is constructed during the conversion from the CST to the AST. As the CST is traversed, new function and variable declarations are added to the Symbol Table, and each node in the AST referencing these functions and variables are given a pointer to them in the Symbol Table.
Symbol Table Structure
The Symbol Table (defined in SymbolTable.h and SymbolTable.cpp) stores three sub-tables.
The first table stores the string literals the program requires. Its data type is an std::vector of std::pair of strings.
The first string in the pair is the id of the string literal that will end up in the final assembly file. This id is used in the assembly file to reference the string literal’s location in the .text section. The second string in the pair is the actual string value of the string literal.
The second table stores the static variables of the program within a vector of pointers to allocated VariableSymbolTableEntry objects.
The third table stores the functions of the program within a vector of pointers to allocated FunctionSymbolTableEntry objects.
While type checking wasn’t a part of this project, the Symbol Table is still important to coordinate string literals, function arguments, and the memory location offsets of variables spilled to the stack.
Assembly Generation
After constructing the Abstract Syntax Tree and building the symbol table, the next step is generating the assembly code.
Three Address Code (3AC)
While it is possible to generate correct assembly code straight from the AST, this unoptimized scheme would require storing and loading the results of every intermediate operation to and from memory. To improve upon this, we first generate instructions in an intermediate form called Three Address Code (3AC). The basic format of most 3AC instructions are:
A = B op C
where A is the destination register to store the result, B and C are registers that store the inputs, and op is the operation being performed on the data in B and C. The 3AC used in this compiler can reference four types of operands:
- Literals
- These are numbers, usually to be used as an input to some instruction
- Machine Registers
- These correspond directly to 32-bit ARM registers (e.g. r1, r2, r3, lr, pc etc.)
- User Variables
- These operands correspond to variables defined in the program by the user
- Temporary Registers
- When generating assembly for an expression, a machine register is not immediately assigned to the result. Instead, a new temporary register is used. 3AC allows unlimited temporary registers.
The first three operand types seem perfectly logical, however, why would one need temporary registers? Well, in the worst case, the number of registers needed to store all the intermediate values for a complex expression is unbounded. For example, consider a balanced AST of the expression ((a + b) * (a – b) + (a + 2) * (a – 2)) * … + ( … ( … ) … ). The compiler can create unlimited temporary registers to sort out machine register assignment later.
Generating Three Address Code (3AC)
To illustrate the generation of 3AC, we will start with Expressions. Given the following MiniJava code:
Which produces the following AST:
In this AST diagram, every name followed by double parentheses is an object. We will start with the first assignment statement, assigning a value of 32 to a. To parse an expression, the compiler traverses the expression tree in post-order, which guarantees that before 3AC is generated for an Expression node, the 3AC for all of its children are generated first. There is only one Expression node here, and it has no children, so its 3AC will be generated as:
with its result location being stored in the temporary register $t0.
Its parent, the AssignmentStatementASTNode will then generate its own 3AC, using the 3AC of the child. It knows that the result of the Expression node is stored in temporary register $t0, so it moves the result into the variable it is assigning to, in this case variable a. The 3AC of the AssignmentStatementASTNode is now:
A similar process is followed to generate the 3AC for the assignment to variable b:
Generating 3AC for the last assignment statement is a little more interesting. As stated before, 3AC is generated for each Expression node in post-order. (The sequence of events in the diagrams are simplified as a depth-first traversal for simplicity when it is really post-order) This guarantees that the child nodes of every node generate their 3AC before the parent nodes generate their 3AC.
For the last assignment statement, the variable assignments and integer literals are fed into their parent nodes by their result location. This result location is used as input to the 3AC for the parent node:
Then those result locations are used to generate the 3AC for the NormalOperationExpASTNode. NormalOperationExpASTNode is a class which represents several types of ‘normal’ assembly operations: addition, subtraction, multiplication, division, binary AND, and binary OR. These operations take in two inputs, and give an output. In this example, the operations used are addition, subtraction, and multiplication. As shown in the diagram, the result locations of the expression inputs are used in the generated assembly operations.
The highlighting of the generated 3AC corresponds to the color of the node that generated it. This allows you to see how the 3AC generated from lower nodes propagates up through higher nodes. Green highlight is from IntegerLiteralExpASTNode, orange highlight is from AssignmentStatementASTNode, yellow highlight is from VariableReferenceExpASTNode, and blue highlight is from NormalOperationExpASTNode.
Each Normal Operation sets its result to be stored in the next unused temporary register. This can then be used by another Normal Operation as its parent. In this way, an arbitrarilty large tree of expressions can be translated into Three Address Code (3AC).
The 3AC from the children is added in sequence before the 3AC that the parent node generates. That way, the expressions the parent node depends upon have already computed their results.
Thus the final generated Three Address Code (3AC) is:
Control Flow
Control Flow statements implemented by this compiler include if/else and while. First, boolean expressions are generated. These are generated much the same way as numerical expressions, however, exceptions are taken for comparison statements. While the AND and OR operations have destination and source registers, the results of comparison operations are not stored in normal registers. They instead change various flags.
To make the comparisons compatible with the boolean operations, we first move a 0x00 (false) into the register that will serve as the result for the subexpression.
Next, perform the comparison instruction. This instruction takes two input registers, and sets the N, Z, C, and V flags.
Finally, to use the result of the comparison instruction, we use a conditional move that corresponds to the desired condition.
This guarantees that the value left in register $t0 is 0 if a is less than b, or 1 if a is greater than b. A similar process is followed for all other conditions.
To generate the assembly for the if/else and while statements, branch instructions and labels are inserted between sections of assembly.
Given the following MiniJava snippet:
This code is compiled as:
You can see that the if/else statement results in three labels after the instructions computing the boolean condition. First the _true0 label is generated, with the code following it being the code executed if the boolean statement is true. Next the _false0 label, with the code following that being the code executed if the boolean statement is false. Finally, the _endif0 label, which marks the end of the if/else statement. The _endif label is used at the end of the true code block to avoid falling through and executing the false condition code. The 0 on the end of all these labels is determined by a class specific static variable which ensures that all the labels in the entire program pertaining to if/else statements are unique to that statement.
Calling Convention
In order to call an ARM assembly subroutine, we must first understand calling convention. When an assembly program calls a subroutine, the program does not necessarily know which registers the subroutine uses, and the subroutine does not know what registers the caller program is using. If this problem is ignored, a subroutine may overwrite data that the caller program was using.
To rectify this situation, the calling program and the subroutine must agree upon which registers to save before running the subroutine.
One possible scheme to accomplish this is to save all the registers to the stack in the calling program. This would make all the registers ‘caller-saved registers’. This approach would produce correct code, however, it may be a bit inefficient. If a subroutine only uses a few registers, all the loads and stores made by the program to save and restore the registers is slow.
Conversely, the subroutine could save all of its registers before executing its code, then restoring them before returning. However, this is similarly inefficient. If the caller is not using a register, but the callee is, the callee will save and restore it unnecessarily.
The standard calling convention used with 32-bit ARM is that the first four registers (r0-r3) are caller-saved registers, and the rest are callee-saved registers. This strikes a balance between the two aforementioned approaches.
To handle argument passing, the first four arguments are stored in r0-r3, and the rest of the arguments are stored on the stack. For project 5, all function calls have four arguments or less.
The return value is returned in r0.
Function Calls
In the compiler, a function call can be either an ExpASTNode (if the call is part of an expression), or a StatementASTNode (if the call is on its own). The compiler handles both very similarly.
To generate 3AC, the compiler first generates the 3AC for all of the function arguments. If the argument is another function call, the result of that function call (stored in r0) is moved into the correct argument register.
Register saving and restoring is done after Coloring, not during 3AC generation. This is because we do not know precisely which registers are being used in the caller and callee.
Register Assignment
Three Address Code (3AC) is generated using symbolic registers, however, this code will not assemble. We need to take these symbolic temporary registers, and assign them to physial register in the CPU.
Liveness Analysis
Say you have a CPU that has two registers, r0 and r1. You want to translate the following program into assembly code:
As you might notice, there are more variables than our CPU has registers. Fortunately, there is a way to accomplish this without spilling, a term used to describe ctemporarily storing the value of a variable to the stack:
As the variable a is no longer being used in the program after line 2, c can then be assigned to the register c was being held in. The same is true for c and d in the line after.
It’s pretty easy to identify when we stop using the values of variables in straight line programs like this, but what if we want to do the same in programs that have many different branches? The solution is to perform Liveness Analysis, an algorithm which can determine when we need to keep the value of a variable, or if it is safe to overwrite.
USE/DEF Set Computation
The first step to performing Liveness Analysis is to calculate the USE and DEF sets of each instruction. The USE set of an instruction is the set of all operands that it uses as inputs, and the DEF set is the set of all operands that are defined, or changed, as a result of the instruction.
For example:
This instruction is using the contents of r2 and r3 (thereby going in the USE set), and defining r1 (thereby going in the DEF set).
The utility of calculating these properties will be clear in a moment, but first let's look at how these sets are calculated within the compiler.
need short section on Instruction objects???
Each class inheriting the abstract class Instruction contains methods for computing the USE and DEF sets, as this is done on a per instruction basis.
During Liveness Analysis, the vector of instructions is iterated through, calling the get_use_set() and get_def_set() methods for each instruction. These sets are then used during Liveness analysis.
The Algorithm
After calculating the USE/DEF sets, we next need to calculate the live-in sets and live-out sets. A variable is live-in at node n if it is either used in node n (a ∈ use[n]) or it is live-out at that node while not being defined (out[n] - def[n]). The second condition essentially means that a variable will be live-in for a node n if there is a path from node n to another node that uses that variable.
We can write this in set notation as:
in[n] = use[n] ∪ (out[n] - def[n])
A variable is live-out at node n if it is live-in at one of the successors of n.
We can write this definition in set notation as:
out[n] = ⋃ { in[s] | s ∈ succ[n] }
Given these definitions, it seems impossible to calculate the live-in and live-out sets of the nodes, because the calculation of the live-in set relies on the live-out set, and the calculation of the live-out set relies upon the live-in set. It turns out it is correct that the live-in and live-out sets cannot be calculated for each node independently. In fact, we are going to apply these set rules to each node of the Control Flow Graph in an iterative manner, until no changes occur between iterations.
To visualize the process, we have a table where each row is a node of the program. The USE, DEF and successor (SUCC) sets are listed alongside each node.
| iteration | 0 | 1 | 2 | 3 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| node | USE | DEF | SUCC | live-out | live-in | live-out | live-in | live-out | live-in | live-out | live-in |
| 5 | c | ∅ | ∅ | ∅ | ∅ | ∅ | c | ∅ | c | ∅ | c |
| 4 | a | ∅ | 2, 5 | ∅ | ∅ | c | a c | a c | a c | a c | a c |
| 3 | a b | c | 4 | ∅ | ∅ | a c | a b | a c | a b | a c | a b |
| 2 | a | b | 3 | ∅ | ∅ | a b | a | a b | a | a b | a |
| 1 | ∅ | a | 2 | ∅ | ∅ | a | ∅ | a | ∅ | a | ∅ |
We start applying the set rules to the last nodes of the program, and continue upwards. This creates the reverse propagation effect, where the live-in of nodes that use variables are defined, and that live-in is propagated upward to the live-out of the previous node, and so on, until it is defined. For this reason, the nodes in the table are listed in reverse order of the program.
For the first iteration, we initialize the previous iteration of live-in and live-out sets as the empty set for every node. We start by calculating the live-out set for iteration one. Remember, the live-out set is calculated as the n-ary union of all live-in sets of the node’s successors. Because node 5 is a return statement, it does not have any successors. Therefore, the live-out of node 5 remains the empty set. Next, we calculate the live-in set of node 5 as its USE set unioned with variables in the live-out set and not in the DEF set. The variable c is in the USE set, and the live-out and DEF sets are empty, so the live-in set of node 5 becomes c.
This process is repeated down the table for each node. Once the end of the table has been reached, the process is repeated in a new iteration, until the previous and current iteration are the same.
Interference Graph
Using the live-in and live-out sets calculated in the Liveness Analysis stage, we can construct a useful data structure called the Interference Graph. The interference graph is an undirected graph, where the nodes of the graph represent the variables of a program. The edges of the graph represent interferences between two variables. Two variables are interfering if at any point in a program, both variables appear in the same live-in or live-out set. What this means is that the value of both variables are still needed at that point in the program, thus they must not be assigned the same register. Here is the Interference Graph for the above program.
You can see that there is a connection between nodes a and b, and another connection between nodes a and c. A further inference that you can draw from this graph, is that variable b and c can be assigned the same register. This observation dovetails nicely into the next section.
Graph Coloring
After building the Interference Graph, we can finally get on to allocating registers to variables. One method of assigning registers is called Graph Coloring. Graph Coloring is a theoretical mathematical problem that asks, given a graph, to find the lowest number of colors that can be used to color all the nodes in the graph without any two connected nodes having the same color. This is a NP-hard problem.
Graph coloring is directly analogous to our problem of register assignment, because the graph we wish to color is the aforementioned Interference Graph, while the ‘colors’ are the physical registers of the CPU we are compiling for.
Given the NP-hardness of the problem for graphs greater than 3 nodes, a faster algorithm is required. Enter the Chaitin-Briggs register allocation algorithm, at its core, the degree < K rule:
Suppose a graph G has a node n which has a degree (number of connections) of less than K . If it is possible that the subgraph G - n (graph G without node n) is possible to color with K colors, then the original graph is possible to be colored with K colors. The rule is obvious in the reverse direction. If a graph G is K-colorable, then it remains K-colorable if a node n is added with degree < K. The degree of n being less than K implies that there is guaranteed to be a color that n is not connected to, therefore n can be colored with that color.
This rule dovetails into Chaitin’s Algorithm for Graph Coloring. The algorithm is as follows:
The degree < K rule guarantees (I think???) that if no spills occur when pushing the nodes onto the stack, then every node can be assigned a color (physical register). When assigning registers, we preferably want to use registers that have already been used in the program, so that when we make function calls, we need to caller save as few registers as possible. In this spirit, we also want to prioritize using callee saved registers, so that the current function doesn’t have to worry about caller saving too many variables on each function call.
Maybe later I will add a nice animation of the algorithm. In the meantime, check out Rasmus Andersson's visualization.
Spilling
If Chaitin’s Algorithm encounters a node that has a degree of K or more, it cannot be colored and thus must be spilled. As previously mentioned, spilling is when the value of a variable is temporarily stored on the stack so that another variable that is needed can replace it. However, this moves the data to main memory in most architectures, which is slow, therefore spilling should be minimized. (In modern CPU architectures, it is very likely that the detrimental effect of a low number of spills will be completely negated through hardware techniques such as large L1 caches. )
In 32-bit ARM assembly, every time a spilled variable is used in an operation, a load instruction must be inserted before it is used:
Unfortunately, spilling is a very difficult problem. Theoretically, in a straight-line program with no branches, a solution could be found that minimizes spilling. Loops negate this, because varying runtime inputs to the program may change the control flow of a program. Suddenly, a single loop could dominate the runtime of a program in a specific run, and if variables are being spilled and restored to registers inside the loop, this will be a non-optimal situation.
Because of the complexity introduced by loops, and other factors, we must determine spill candidates through heuristics. One such heuristic is a cost-benefit analysis. The cost in this case is the number of loads and stores performed at runtime as a result of spilling a certain variable, while the benefit is how many interference edges can be removed from the Interference Graph as a result of spilling that variable. For simplicity, we assume that a spill candidate will be “spill everywhere”, meaning that every time the value is used, it will be loaded. It would be possible to spill a single variable at only certain locations of the program, but this adds additional complexity.
Estimating the spill cost is difficult, because we do not know how many iterations will occur in a loop at runtime, nor do we know the probability that a certain conditional branch is taken. Therefore, we have to estimate. For this simple spilling optimization technique, we can assume that the number of times each loop iterates is a constant, such as 10. Therefore loops at n depth will have an estimated iteration count of 10^n. The probability of taking a branch is also estimated at 50%.
Once the cost is calculated for each variable, the variable with the best cost/degree ratio is selected for spilling.
After taking into account the complexity of determining where and when to spill, it is easier to appreciate the possible benefits of Profile-Guided Optimization.
For CS352, it was not required to implement spilling because it is a cut down version of the graduate course CS502. All input code to be compiled was assumed to have variables less than or equal to the number of registers available. However, I think it would have been fun to write a spilling stage. If I come back to this project in the future, that is where I would pick up.
Caller and Callee Saved Register Assignment Optimization
Recall that before a program calls a function, it must save the contents of the caller-saved registers that it still needs to avoid data being overwritten by the called function. Before the called function runs, it needs to save the contents of the callee-saved registers that it will use. If we know which functions are leaf functions (functions that do not call other functions), we can implement an optimization. If we know that a function will never call another function, then inside that function, we should prioritize the use of caller-saved registers. Since this function never calls another function, those registers are essentially free, they never have to be saved to the stack.
The converse optimization also applies. If we know that a certain function calls other functions, we should prioritize using callee-saved registers to avoid saving registers on every function call.
??maybe put illustrative code block here?? the problem is that the code for this part isn't that illustrative
This code loops through the program and determines how many times the current variable being colored interferes with function calls. If the variable interferes with at least one function call, it is prioritized to be assigned a callee saved register. This is still a heuristic however, because it may be the case that a function call interfering with the current variable almost never gets called at runtime because of a conditional block, thus there would be little reason to assign the variable to a callee-saved register.
Additional Optimizations Performed
Some additional optimizations were added to the register assignment.
First, is removing nodes from the interference graph by lowest degree to highest degree. Instead of simply finding any node with a degree < K, the node with the lowest degree should be removed from the graph first. This places the nodes with the lowest degrees on the bottom, ensuring that the nodes with the highest degrees, and thus the most constraints, get colored first. Nodes with lower degrees get put on the bottom of the stack, and are thus colored later, effectively making the low degree nodes adapt to the colors of the high degree nodes.
The second optimization added is taking into account copy preference. In a program, if there are move operations involving at least 1 symbolic register, then it is possible to assign that symbolic register to have a copy preference with the other register in the move operation. This will prioritize the register assignment of that symbolic register with the assignment of the other operand. As an example, say this code appears in the program.
After the interference graph is generated, we loop through all the instructions, and if there is a move to another register, we assign a copy preference between those two nodes if they do not interfere. In this instance, symbolic register $t1 would be prioritized to be assigned r0. This would result in the following code:
After register assignment, the redundant move can be eliminated which would then make the code:
Additional Possible Optimizations
Say we have a program where a variable is assigned a value at the beginning of a program then used shortly after. Later in the program, it is assigned a new value and used later.
Example:
When calculating Liveness and building the Interference Graph, it would be determined that the variable x interferes with a and c. However, x was reassigned in the middle of the program, so it would be possible to assign the first definition and subsequent use of x to one register, while assigning the second definition and subsequent use of x to another register. By doing this, we would eliminate interference between x and b, thus making register allocation slightly easier, and possibly saving the allocation of an unused physical register.
This example should reveal the insight that we should not actually be building the nodes of the interference graph based on variables, or even symbolic registers, they should be built on live ranges. In the example, x has two distinct live ranges. The optimization performed in which these separate live ranges can be assigned separate registers is called live range splitting.
This was not implemented in the final compiler as none of the test inputs required such an optimization to reduce loads/stores.
Conclusion
Errata
In the final version of the project, the instructions generated for integer division are not correct. No provided test script contained division, and I wrongly assumed that the integer division instruction mnemonic was div instead of sdiv.
While going through the code to write this report, I realized that I am treating copy preference edges in the Interference Graph as interfering when calculating the degree of a node. This should not affect the generated code that much, but it might change the order in which nodes are pushed onto the coloring stack, perhaps leading to a suboptimal graph coloration.
Potential Improvements
This was my first large scale C++ project, so I had to learn the syntax, features and conventions as I went along. There are surely areas in which the code could be improved in readability.
I did not pay attention to memory management at all. Tracking of objects and deletions are probably needed.
The AST is traversed in post-order when generating 3AC by each expression or statement node calling the gen_3AC() function of its children nodes before resolving its own gen_3AC() function. This was a very easy way to program the post-order traversal, but it limits the expression/statement depth of the code being compiled to the stack size of the machine the program is being run on. This should rarely be a problem, as the expression/statement objects aren’t very large, and runs of consecutive statements are vectorized (not in classic AST tree form).
The flex → bison → Concrete Syntax Tree C structs → Abstract Syntax Tree C++ objects could be more refined or simplified, as this was an artifact from rewriting the project from C to C++.
Final Thoughts
I would have gotten 100% on this project if I hadn't overlooked my integer division mistake. All my optimizations to reduce memory loads and stores put me at the top of the class for Project 5.
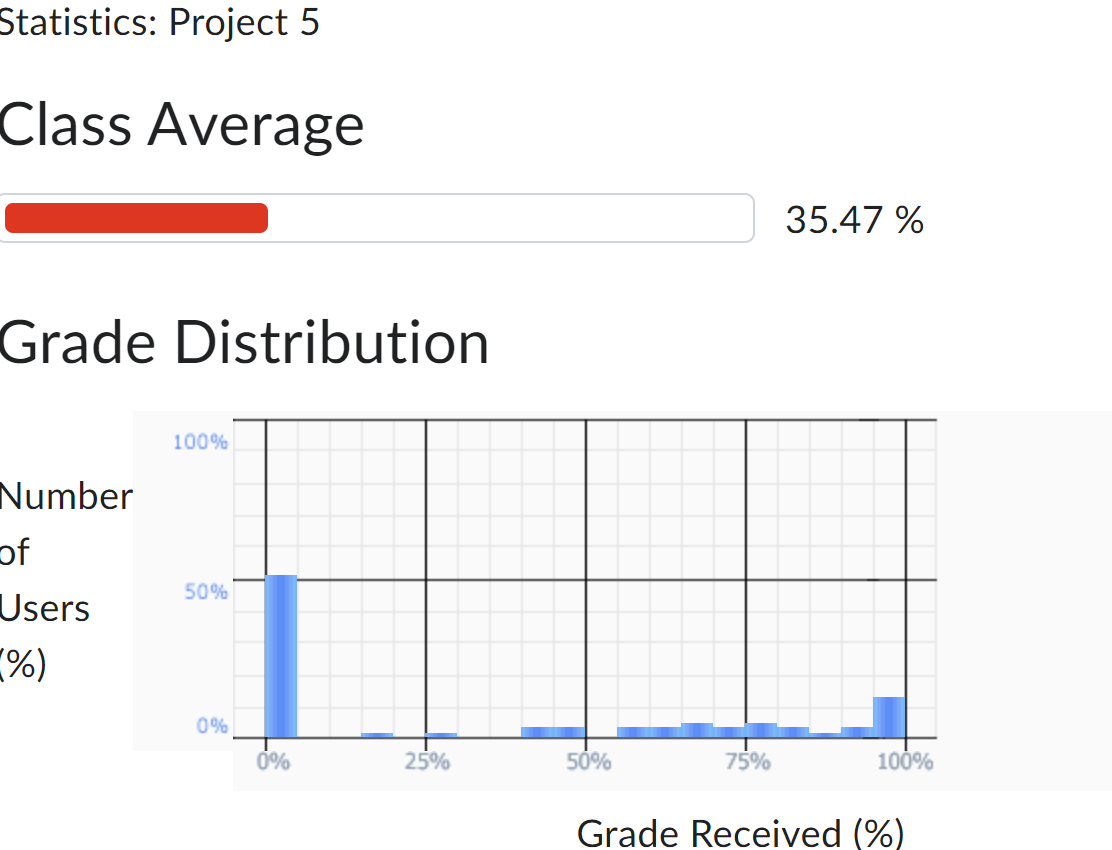
For some reason, over 50% of the people enrolled in the class got a 0% on Project 5. This is quite baffling, as if they had completed Project 4, they could have simply submitted that for Project 5 and gotten a 30%. This was because there were no new features in P5 besides register assignment optimizations. I guess the series of projects that build on each other was just too difficult for some people to hack.
Despite causing a large amount of stress, I think this project was very useful for me. I improved my C++ skills, and now I know about all the stages of a compiler, fitting in another puzzle piece of how computers operate. In my opinion, the best way to learn about compilers is to write one.
“You really understand something until you program it.” - Professor Gustavo Rodriguez Rivera